Natural Logarithm
The natural logarithm
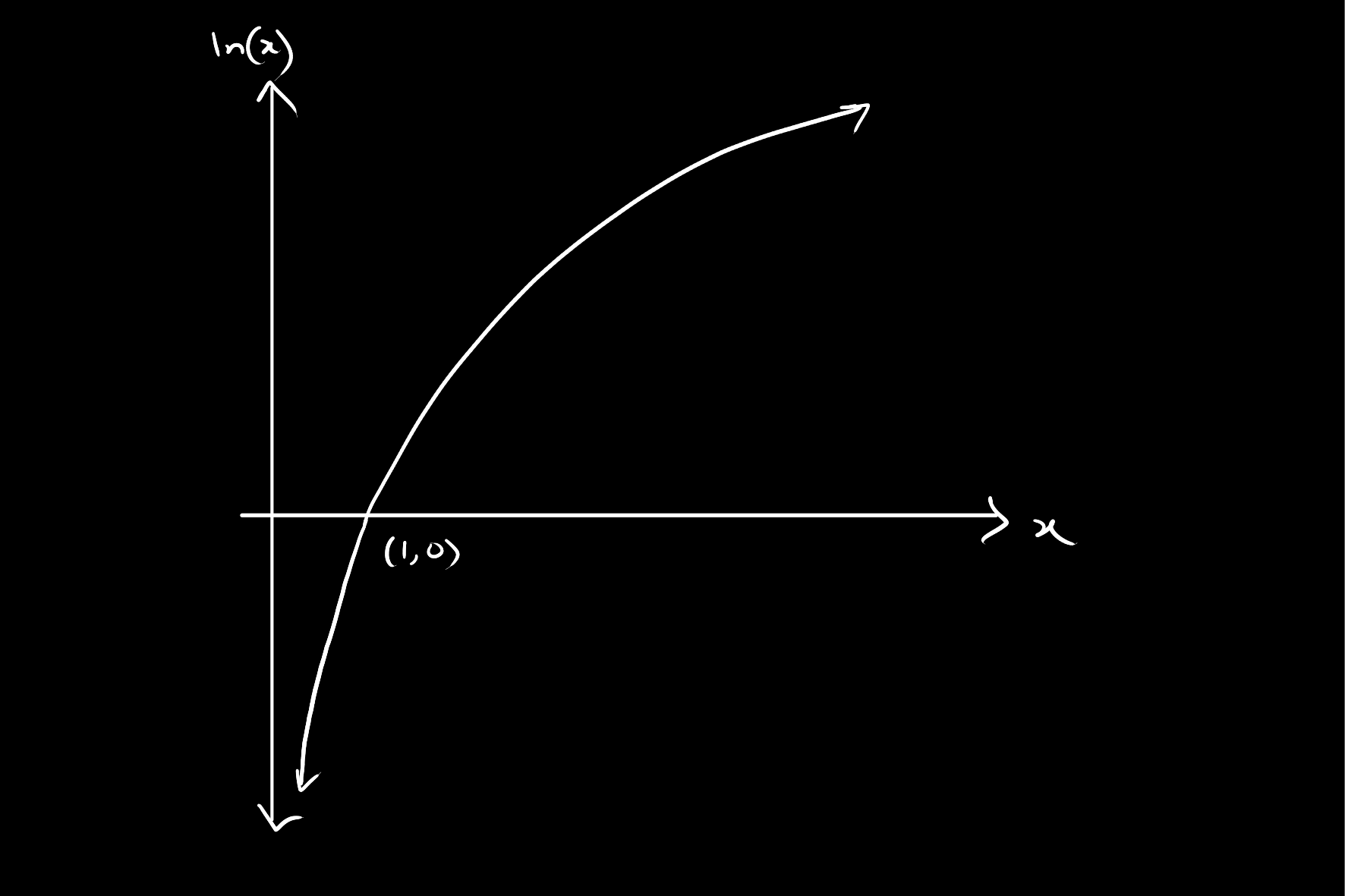
Properties
Proof
Now we use a substitution of
Proof
We can use a substitution of
Note that this proof requires that
Proof
Consider the area under
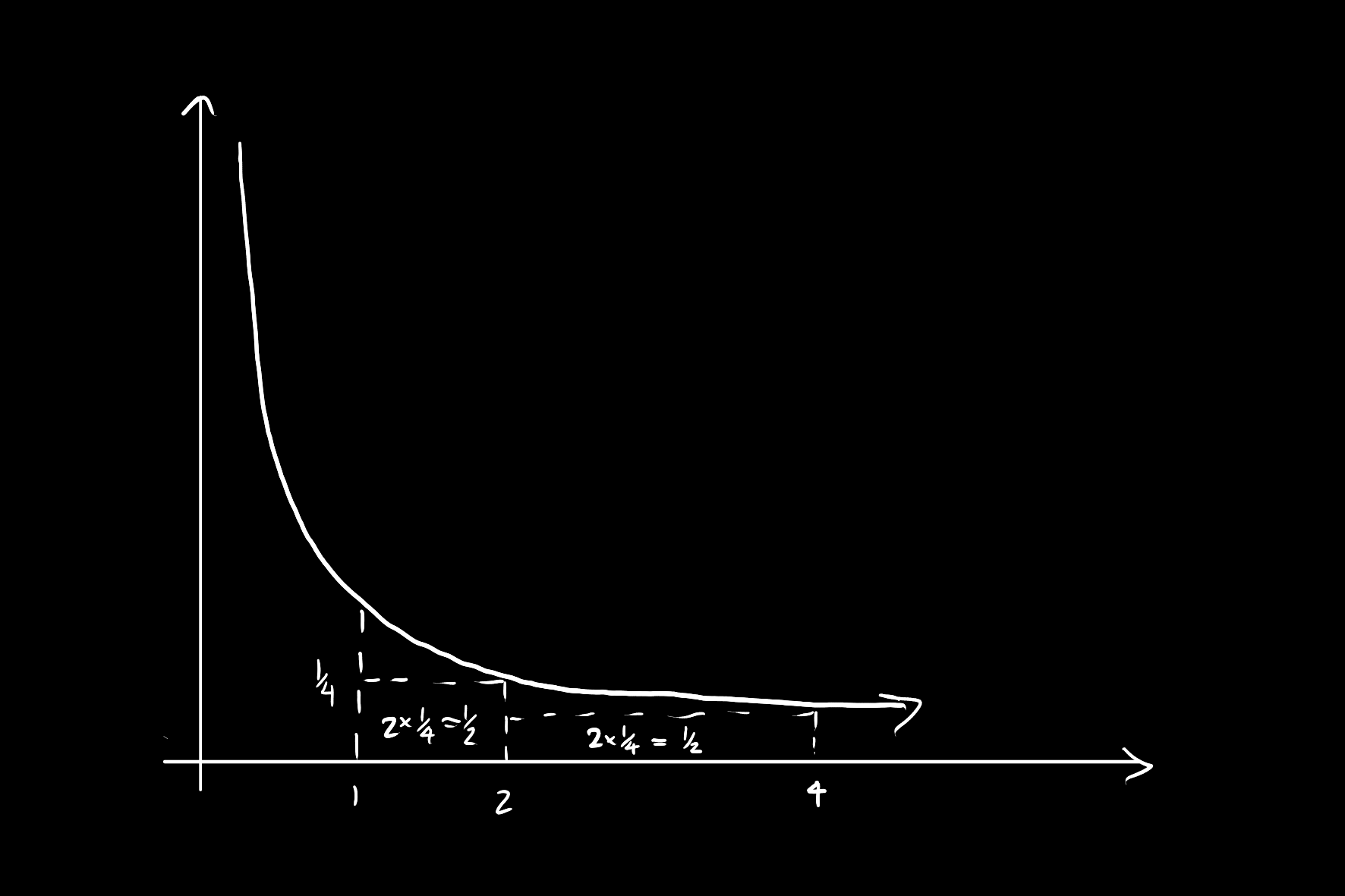
If we then evaluate this for
Then since
The natural logarithm

Now we use a substitution of
We can use a substitution of
Note that this proof requires that
Consider the area under

If we then evaluate this for
Then since